De wiskundige die paus werd

Pausen worden niet gauw vergeten. Om te beginnen wacht je als paus een begrafenis met koninklijke allure in de St Pieter te Rome, de basiliek gebouwd op het graf van Petrus. De geliefde Johannes Paulus II was in 2005 de laatste paus die deze eer te beurt viel.

Vroeger placht men dode pausen elders in Rome bij te zetten, in de Johannes Lateranen basiliek. Toen deze statige kathedraal, op een steenworp van het Colosseum, in de zeventiende eeuw wegens achterstallig onderhoud dreigde in te storten besloot paus Innocentius X, met de vieringen van het Heilig Jaar 1650 in het vooruitzicht, de boel maar eens grondig te laten restaureren. De restauratiewerkzaamheden werden echter gehinderd door onvoorziene omstandigheden: de pauselijke graven lagen danig in de weg.

Heilige grond of niet, de werklieden zagen zich genoodzaakt een aantal sarcofagen open te breken. Waaronder die van paus Sylvester II, die er in 1003 begraven was. Sylvester stond bekend als ‘de magische paus van het jaar 1000’: zijn gebeente rammelde in zijn graf, telkens als er een regerend paus op het punt stond te overlijden. Zijn stoffelijke resten trof men in goed geconserveerde staat – het lichaam verspreidde een aangename geur. Een wonderbaarlijke toestand. Voor even althans, want door het contact met verse lucht verbrokkelde het lichamelijk omhulsel binnen een mum van tijd tot stof. Al wat overbleef was zijn rammelend gebeente.

Gedurende zijn korte pausdom had Sylvester gepoogd de Roomse kerk te ontdoen van corruptie en decadentie. Van dat streven kwam niet veel terecht, maar zijn geestelijke nalatenschap is niet vergeten: precies duizend jaar na zijn dood voerde paus Johannes Paulus II in diezelfde basiliek een herdenkingsmis op, met veel vertoon. “Sylvester herinnert ons eraan”, sprak de paus, “dat intelligentie een wonderbaarlijke gave van de Schepper is”. Want diens intelligentie was vermaard: Sylvester was maar voor even paus, maar voor altijd wiskundige.

Kerfstok

Aan een zijrivier van een zijrivier van de Dordogne ligt het slaperige stadje Aurillac. De voornaamste bezienswaardigheid is de oude abdijkerk Saint-Géraud, een overblijfsel van de benedictijner abdij die graaf Géraud in de negende eeuw op zijn landgoed deed grondvesten. De legende wil dat zieken het water waarmee de weldoener zich waste opvingen om zich ermee te genezen. Een verlamd kind dat men het vuile waswater over de benen sprenkelde kon waarachtig weer lopen. Reden genoeg om de puissant rijke Géraud heilig te verklaren.

Het klooster Saint-Géraud heeft echter nóg een claim to fame: in het jaar 963 verwelkomde het een armlastige wees als lekenbroeder. Gerbert was zijn naam, en hij zou het schoppen tot paus. Paus Sylvester II.

Een doorsnee klooster werd bevolkt door lekenbroeders en monniken. Monniken, doorgaans afkomstig uit gegoede families, deden vrome arbeid: bijbelstudie en boeken kopiëren, dat soort dingen. Lekenbroeders deden gewichtiger werk: land bewerken en latrines legen, dat soort dingen. Toen Gerbert op zijn zestiende toetrad tot Saint-Géraud ondervond hij het aan den lijve, maar zijn vlijt en vernuft liepen zozeer in het oog dat hij opklom tot monnik en zich mocht wijden aan het verwerven van kennis over Gods natuur. Daarna ging het snel.

Gerbert mocht naar de vermaarde kathedraalschool van Vic, de Catalaanse bisschopsstad. Catalonië grensde aan al-Andalus – het grootste deel van Spanje was sinds 711 een islamitisch kalifaat. In tegenstelling tot christelijk Europa kon vrijwel de gehele islamitische bevolking lezen en schrijven, en werden de wetenschappen beoefend op hoog niveau. Waar een beetje christelijk klooster al blij mocht zijn met duizend boeken, was de bibliotheek van Córdoba met 400.000 boeken de grootste ter wereld.

Wiskunde was in Europa een onderontwikkelde tak van sport, maar vierde in al-Andalus hoogtij. In Catalonië rekenden wiskundigen met Romeinse cijfers, in al-Andalus met (de later zo genoemde) Arabische: een wereld van verschil. Rekenen met cijfers was een nieuwigheid van belang. Europa rekende met onhandige symbolen – áls er al werd gerekend.

Aanvankelijk dachten we überhaupt niet in aantallen. Eén telde niet – een neus, een geit, een geroosterde vis: er viel niets te tellen. Een heleboel, dat telde je ook niet – een kudde geiten, een boom vol bessen: gewoon, veel. En dan had je nog ‘een stuk of wat’: je kinderen, de kippen, een handjevol bessen. Maar in precieze hoeveelheden denken, dat was niet nodig.

Op enig moment zijn onze voorouders besef van aantallen gaan ontwikkelen. Je kon bij benadering vaststellen of de hoeveelheid gevangen vis voldoende was voor de monden die je moest voeden. Maar om te checken of er geen geiten van de kudde waren afgedwaald volstond schatten niet – en dus leerden we tellen. Tellen deden we door te turven, op een afgebroken tak of een gevonden bot waar je kerfjes in sneed. Er zijn kerfstokjes gevonden van 37.000 jaar oud.

Maar tellen is nog geen wiskunde.

Computer des Doods

De eerste vondst van wiskundig belang stamt van 15.000 jaar later: het Ishango-beentje. Jean de Heinzelin de Braucourt, een geoloog die in 1960 door het Koninklijk Belgisch Instituut voor Natuurwetenschappen voor bodemonderzoek naar Congo werd gestuurd, vond aan de oever van een Nijlmeer een bavianenbotje uit de steentijd. Gebruikt voor turven en tellen, maar bij nader inzien ook voor rekenen, zoals verdubbelingen en halveringen.

De pre-columbiaanse beschaving in Peru beklom 5000 jaar geleden een hogere trap van rekenen. Een quipu is een soort antieke telcomputer: strengen van aaneen geregen koorden waarin je knopen legde om aantallen aan te duiden. Klinkt simpel, maar ze dienden als administratieve telramen, met een heus decimaal stelsel: de onderste knopen gaven de eenheden aan, daarboven gelegen knopen de tientallen, enzovoort. De kleur van de koorden en de onderlinge afstand tussen de knopen werden gebruikt om getallen voor verschillende categorieën bij te houden. Een codering die doet denken aan eenvoudige computeralgoritmes (een hedendaags computerfile-management systeem luistert naar de naam quipu).

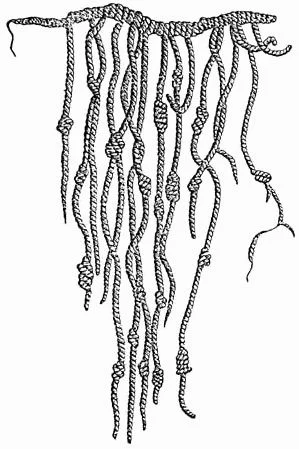
Om te kunnen rekenen hoef je niet te kunnen schrijven: de Inca’s, die de quipu overnamen, kenden geen schrift, hun complexe beschaving ten spijt. Maar met behulp van de quipu (die wel duizend koorden kon bevatten) hielden ze verhalende archieven bij. Allerlei bijzonderheden uit de Inca-geschiedenis staan erin gecodeerd: bouwplannen, kalenders, dansvoorschriften, en de sinistere rekenmachine des doods. Tijdens plechtige ceremonies offerden de Inca’s opgeschoten pubers om de goden gunstig te stemmen (slachtoffer zijn was een hele eer); met behulp van quipu’s werd het jaarlijks quotum aan zulke rituele slachtingen bepaald.

Cijferen

Schrijven is dus geen voorwaarde om wiskunde te bedrijven – maar het helpt wel, en bij de Babyloniërs met hun spijkerschrift ging het met de wiskunde dan ook vlot vooruit. Naast de spijker gebruikten ze een ‘<’-teken om te cijferen. De cijfers 1-9 gaf je aan met 1-9 spijkers; de cijfers 11-19 met < gevolgd door 1-9 spijkers; 21-29 met << met 1-9 spijkers, enzovoort. Hun kleitabletten, pakweg 4000 jaar oud, bevatten de eerste geschreven wiskunde. Hele tafels van vermenigvuldiging staan er op.

Niet veel later mengden de Egyptenaren zich in de strijd met hun hiërogliefen. Alexander Rhind, behalve rechter ook verzamelaar van oudheden, bracht in 1858 de winter door in Egypte. Rond die tijd waren daar overal avonturiers actief met illegale opgravingen, op jacht naar lucratieve vondsten. In de ruïnes van een tempel, opgetrokken door Ramses II bij Thebe (het tegenwoordige Luxor) op de westoever van de Nijl, troffen ze een papyrusrol van ruim 5 meter lang, die ze op de markt van Luxor verkochten. Rhind, een Schot met een scherp oog voor waardevolle oudheden, zal ongetwijfeld hebben afgedongen. In elk geval heeft hij zijn naam ermee weten te vereeuwigen: de Rhind Papyrus zou roem vergaren, vanwege de wiskunde die men er op aantrof (na ontcijfering van de hiërogliefen, vele jaren later).

De karakters bleken niet alleen getallen te symboliseren, maar ook breuken. Handig, want in plaats van geld kenden de Egyptenaren ruilhandel, waarbij je goederen moest verdelen over meerdere mensen. Stambreuken (met 1 als teller: 1/n) maakten alles eenvoudig: wil je 1/10 van iets hebben dan snij je het in tienen en klaar ben je. De Egyptenaren drukten alles wat los en vast zat uit als een som van stambreuken. Had je bij een feestmaal 3 vissen te verdelen over 8 gasten, dan deelde je elke vis in achten en gaf je elke disgenoot 3 stukjes – 1/8 + 1/8 + 1/8 – iedereen exact evenveel, en nog in gelijke porties ook. En voor het snijwerk had je slaven.

Deze cijferkunde voorzag in een praktische behoefte. Voor de Babyloniërs en de Egyptenaren boden de rekenexercities vooral een handig instrument voor vraagstukken uit de praktijk. Na de jaarlijkse Nijloverstromingen moest bepaald worden hoe de akkers weer netjes af te scheiden; dergelijk gecijfer kwam dan mooi van pas.

Bij het opkomen van de Griekse beschaving verschoven de praktische toepassingen naar de achtergrond – die lieten de wiskundigen over aan werklieden. Hen ging het om zuivere, abstracte wiskunde. Daarom brachten ze wat meer systeem in de letternotatie die ze hanteerden voor getallen. Letters uit hun alfabet vormden achter elkaar gezet een getal. Er waren negen letters voor de cijfers 1-9, negen andere voor 10-90, en nog negen voor 100-900. Duizendtallen kreeg je door een komma te zetten voor de letters voor 1-9. Zo schreef je 33 en 3333 als λγ en ,γτλγ. Decimaaltekens waren er niet; daarvoor in de plaats gebruikte je Egyptische stambreuken als α/βγ. Ook het getal nul bestond nog niet. En getallen groter dan onze 9999, die konden niet.

Zuiver, ja – handig, nee. De praktisch ingestelde Romeinen gebruikten liever Romeinse cijfers dan Griekse letters. Het tellen van steentjes of muntjes gaat een stuk vlotter als je ze op elkaar stapelt in hoopjes van vijf of tien. Elk hoopje kreeg z’n eigen Romeinse letter: V en X. Gooi V hoopjes van X op een grote hoop en je hebt L, enzovoorts. Voor rekengebruik in het dagelijks leven hadden ze bovendien een heel handig rekeninstrument, de uit China overgewaaide abacus (een variant van het telraam – als kind leerden we er nog mee rekenen). In een bord met zand tekende je naast elkaar de letters M, C, X en I. Duizendtallen, honderdtallen, tientallen en eenheden gaf je aan door onder de M, C, X of I het gewenste aantal keitjes (calculi) in het zand te leggen. Legde je een calculus bóven het cijfer, dan telde je er vijfmaal dat cijfer bij op. Drie calculi onder de X en één boven de I betekende XXXV. Zo kon je alle getallen van 1-9999 aangeven. Het grote voordeel van de abacus was dat je er heel visueel mee kon rekenen – je ziet het voor je.

Tijdens het verval van het Romeinse rijk raakte de abacus verloren – de Vandalen hadden er geen oog voor. Gelukkig namen de wiskundigen uit het mohammedaanse rijk de abacus gewoon opnieuw over van de Chinezen. Bovendien leerden ze gebruik te maken van een numeriek stelsel, een positiestelsel dat het rekenen flink bleek te vereenvoudigen. Het ging om échte cijfers, de cijfers 1-9 die wij tegenwoordig kennen als Arabische cijfers (al namen de Arabieren ze weer over van Hindoe-wiskundigen uit India). Die cijfers waren heel handig voor grotere getallen: het meest rechtse cijfer was de eenheid, daarnaast het tiental, enzovoorts. U kent het.

Catalonië trok veel profijt van de nabijheid van de moslimbeschaving; er was veel verkeer met al-Andalus. Veel van de wetenschappelijke kennis werd ook op de kathedraalschool van Vic aangeboden. Om zijn dorst naar kennis nader te lessen toog Gerbert later zelf naar Córdoba en Sevilla, waar hij alle Arabische cijfer- en wiskunde als een spons in zich opzoog. En dat zou het Westen weten.

De ontheiligde kathedraal

De geleerde-in-de-dop mocht in 970 mee op pelgrimstocht naar het Vaticaan. Van een latere leerling, Richer de Saint-Remi, weten we dat Gerbert al gauw in het oog liep bij de paus. Paus Johannes XIII onderhield warme relaties met de keizer van het Heilige Roomse rijk, Otto de Grote. Otto was op zoek naar geleerden om zijn hof te verheffen – een beetje keizerlijk hof straalt status uit, en liefst ook wetenschappelijk prestige. Vooral bekwame wiskundigen, daar was lastig aan te komen; daarom had Otto de paus gevraagd uit te kijken naar een goed geschoold iemand. “De ijver en de wil tot leren van de jongeling ontgingen de paus niet”, schreef Richer, en dus “deelde de paus onmiddellijk aan Otto, koning van Duitsland en Italië, mee dat er een jongeman was gearriveerd die de mathematica perfect beheerste en die in staat was deze effectief te onderwijzen”. Gerbert werd onverwijld aangesteld als tutor van de dertienjarige Otto junior.

Werd je geroepen door de machtigste mannen van Europa, dan was dat geen uitnodiging maar een bevel. Maar ook een gunst: tutor aan het keizerlijk hof was zo’n beetje de meest begeerlijk positie die een geleerde zich kon dromen. Aanzien, inkomen, vastigheid, toekomstperspectief, vrije tijd – de tijd van je leven. Gerbert bleef in Rome als adviseur van de keizer en leraar van de jonge monarch. Maar uitdagend was het niet echt – de wiskunde jeukte.

Otto arrangeerde voor Otto junior een huwelijk met een oogverblindende Byzantijnse prinses. Tussen de feestelijkheden door, die drie dagen duurden, ontmoette Gerbert de aartsdiaken van Reims, een eregast. Bij zulke ontmoetingen stond altijd wat op het spel: deuren konden openen of in juist het slot vallen. Vantevoren wist je niet wat zo’n deur verborg, maar het bleek te klikken, ze vonden elkaar in een warme belangstelling voor wetenschap. De aartsdiaken, zelf befaamd logicus, ondernam zelfs een verleidingspoging: kom mee naar Reims, naar de vermaarde kathedraalschool, dan kun je daar niet alleen logica studeren, maar ook wiskunde en astronomie doceren, tegen een riant inkomen.

De poging had kennelijk succes, en kreeg ook de zegen van de keizer: Gerbert vertrok. Al bleef hij met de beide Otto’s warme banden onderhouden – banden die nog van pas zouden komen.

In Reims moest Gerbert zich nog wel waarmaken. Hij onderscheidde zich met een spraakmakende noviteit: hij liet zijn studenten aanvullend op het boekenonderricht oefenen met instrumenten. Rekenkunde bracht hij ze bij met een aangepaste abacus, in de vorm van een tablet die was verdeeld in ‘intervallen’, kolommen die van rechts naar links overeenkwamen met eenheden, tientallen, honderdtallen, duizendtallen, enzovoorts. Onder elk interval zaten vakjes waarin de student de negen Arabische cijfertekens kon verplaatsen. In lege vakjes zat niets: het equivalent van nul.

Voor aanschouwelijk onderwijs gebruikte Gerbert (tot schrik van de kanunniken, tot schik van hun aartsdiaken) de vloer van de kathedraal als een reusachtige abacus, met in stukken gezaagde boomstammen als calculi. Vanaf de orgelzolder riep hij zijn leerlingen opdrachten toe om de schijven heen en weer te schuiven, als levende damstenen op een gigantisch dambord. Grote getallen vermenigvuldigen wordt makkelijk als je niet het hele getal ineens neemt, maar eerst het cijfer van de eenheid, dan van het tiental, honderdtal, enzovoort. Neem een eenvoudige opdracht als 3×23. Eerst de eenheid: hoeveel is 3×3, riep hij zijn leerlingen toe, en liet hen 9 schijven naar de meest rechtse positie schuiven. Daarna het tiental: bij 3×20 moesten er 6 schijven onder het tiental komen. De oplossing was nu een optelsom van twee eenvoudige vermenigvuldigingen: (6×10) + (9×1) = 69. Toen zijn bezwete leerlingen eenmaal doorkregen hoe het werkte ging het vlot vooruit. (Je gaat het pas zien als je het doorhebt, dixit Cruijff.) En Gerbert zag dat het goed was, vanuit de nok van zijn kerk.

Nog vlugger ging het toen Gerbert op elke schijf een cijfer liet noteren: in plaats van een x-tal schijven schoof je een schijf met het cijfer x naar de juiste plaats. Vanaf je orgelzolder zag je meteen de uitkomst. In een handomdraai liet hij zijn zwoegende studenten nu sommen als 643 × 987 uitrekenen. Probeer dat maar eens met DCILIII × IMLXXXVII.

Gerberts boek over rekenen met de abacus werd een standaardtekst in alle kathedraalscholen. Het stelsel was zo doeltreffend dat het al snel werd overgenomen door boekhouders en handelslieden, eerst in Reims en al snel in heel Frankrijk. Zijn nieuwe methode bracht een omwenteling in de rekenkunde teweeg (zo ongeveer zoals bij de eerste Mac-met-muis, die alle type- en rekenmachines overbodig maakte, tijdens mijn studietijd tien eeuwen later).

De wiskundige die Paus werd

Nog meer opzien baarden Gerberts mechanische apparaten. De mensen wisten niet wat ze hoorden: zijn hydraulische orgel overtrof alle vroegere en oogstte alom bewondering. Orgels liepen op lucht, die de organist met zijn voeten door de pijpen pompte (ongeveer zoals het antieke harmonium waarop mijn vader mij de vlooienmars leerde spelen). Had je een gróót orgel, dan had je assistenten nodig om de blaasbalg te bemannen. Gerbert verving mankracht door waterkracht: dat gaf een veel constantere luchtdruk. Bovendien stemde hij de orgelpijpen qua lengte en dikte niet a l’improviste op elkaar af, zoals tot dan toe gebruikelijk, maar rekenkundig, waardoor de harmonischen zuiverder klonken dan ooit tevoren. Zijn oog voor praktisch nut viel bij zijn studenten in goede aarde. Voor abstracte scholastieke debatten had hij minder oog; polemiek en politiek liet hij liever aan de geestelijken.

In de strijd om de Franse troonaanspraken koos de aartsbisschop van Reims partij voor een nieuwe troonpretendent, graaf Hugo van Parijs, boven de oude Karolingische koningslijn. Gerbert was secretaris van de aartsbisschop en behoorde weshalve tot het kamp-Hugo. Tegen wil en dank werd hij onderdeel van een machtsspel dat hem parten zou spelen.

Spoedig nadien overleed de aartsbisschop. Als opvolger benoemde Hugo Arnulf, een Karolinger, in een poging de verdeeldheid te sussen. Een kapitale inschattingsfout. Het begin van een stoelendans die zou eindigen in Rome.

Arnulf kneep een oogje toe toen de Karolingische hertogen de stad Reims plunderden en in puin legden. Ook Gerberts kostbare boeken en instrumenten werden geroofd. Jaren later had koning Hugo afdoende bewijs voor Arnulfs verraad, en verving de aartsbisschop door een loyale en ervaren vertrouweling: Gerbert, de armlastige lekenbroeder.

Hugo’s zoon Robert hield het met de begeerlijke Bertha van Bourgondië, een volle nicht. Kerkwetten stonden echtverbindingen met naaste verwanten in de weg, dus huwde hij Suzanna – twintig jaar ouder en beduidend minder begeerlijk, maar wel met aardige steden en graafschappen als bruidsschat. Na Hugo’s overlijden dwong Robert, nog maar koud koning, Suzanna van hem en van haar bruidsschat te scheiden; hij huwde Bertha alsnog. Maar hiertegen kwam aartsbisschop Gerbert in het geweer: de scheiding was onwettig, het nieuwe huwelijk wegens bloedverwantschap ongeldig. Kerkwet is kerkwet. Het conflict tussen de koning en de aartsbisschop liep zo hoog op dat de paus tussenbeide moest komen. Beide kemphanen kregen een rode kaart: Gerbert werd van zijn bisschopsfuncties ontheven, en Robert en zijn onwettige eega werden geëxcommuniceerd.

De actie van de paus wekte echter het misnoegen van diens neef, keizer Otto III van het Heilige Roomse rijk, die Gerbert nog kende als zijn vaders geliefde leraar. Onder zachte drang (de keizer had paus Gregorius V zelf op het schild getild en kon hem er net zo makkelijk weer aflazeren) bewoog Otto de paus tot Gerbert’s herbenoeming.

De stoelendans kreeg zijn bekroning toen Gregorius overleed. Otto was het gekonkel van de Romeinse politiek beu, en benoemde een vertrouweling tot nieuwe paus: Op 9 april 999 werd Gerbert, de wiskundige uit Aurillac, gewijd tot paus Sylvester II.

Het einde der tijden

De benoeming van Sylvester had een hernieuwd huwelijk tussen kerk en keizerrijk moeten inleiden. Sylvester en Otto deelden een droom: Renovatio imperii Romanorum, een hernieuwde Roomse heerschappij. Het streven was het domein van de katholieke kerk uit te breiden tot aan de grenzen van Europa, en het hele Heilige Roomse Keizerrijk te herenigen onder Duitse vlag. Maar veel verder dan wittebroodsweken kwam de verbintenis niet.

Aanvankelijk ging het voor de wind. Sylvesters missionarissen wisten Polen en Hongarije te kerstenen. Waar Rome onder recente pausen was ondergedompeld in corruptie en seksuele verdorvenheid (deze periode staat aan de wieg van de term ‘pornocratie’), maakte Sylvester korte metten met de wijdverspreide praktijken van concubinaat en simonie onder de geestelijkheid. Rond het jaar 1000 creëerde een vrees voor het einde der tijden onrust en beroering, maar de wiskundige paus zette de grootste paniekzaaiers weg als wappies en complotdenkers en kalmeerde zo de gemoederen. En warempel, op 1 januari kwam gewoon de zon weer op. (Net als duizend jaar later trouwens.)

De paus was een toonbeeld van vroomheid en wijsheid. Maar hij was wel Frans; en de keizer Duits; en daartegen kwam het Romeinse volk in opstand. Dat deed het volk sowieso vaak en graag, opgestookt door de Romeinse edelen, ditmaal met overheersing door buitenlanders als excuus. Otto en Gerbert, op papier de machtigste mannen van Europa, werden de stad uitgejaagd. Bij een poging de macht te heroveren liet Otto het leven. Sylvester mocht wel terugkeren naar Rome, maar onder rebellerende edelen en het rellende volk had hij weinig gezag meer. Een tandeloze tijger.

Twee jaar later zou ook hij het leven laten. Tijdens het opdragen van een mis werd hij onwel en gaf de geest. De wiskundige die paus werd verliet het stoffelijk bestaan zonder blijvende nalatenschap – op zijn rammelende botten en wat zalvende woorden van Johannes Paulus II na.

29 maart 2022

Bronnen ▼